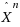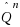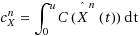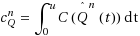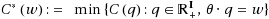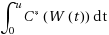Asymptotically optimal interruptible service policies for scheduling jobs in a diffusion regime with nondegenerate slowdown

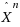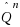A parallel server system is considered, with I customer classes and many servers, operating in a heavy traffic diffusion regime where the queueing delay and service time are of the same order of magnitude. 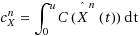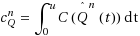Denoting by ${\hat{X}}^n$ and ${\hat{Q}}^n$ , respectively, the diffusion scale deviation of the headcount process from the quantity corresponding to the underlying fluid model and the diffusion scale queue‐length, we consider minimizing r.v.’s of the form $c_X^n={\int }_0^{u}C({\hat{X}}^n(t))\mathrm{dt}$ and $c_Q^n={\int }_0^{u}C({\hat{Q}}^n(t))\mathrm{dt}$ over policies that allow for service interruption. Here, C:ℝ ^I→ℝ+ is continuous, and u>0. Denoting by θ the so‐called workload vector, it is assumed that 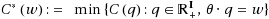$C^{*}(w):=\min \{C(q):q\in {ℝ}_{+}^I,\theta \cdot q=w\}$ is attained along a continuous curve as w varies in ℝ+. We show that any weak limit point of $c_X^n$ stochastically dominates the r.v. 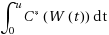${\int }_0^u{C}^{*}(W(t))\mathrm{dt}$ for a suitable reflected Brownian motion W and construct a sequence of policies that asymptotically achieve this lower bound. For $c_Q^n$ , an analogous result is proved when, in addition, C ^* is convex. The construction of the policies takes full advantage of the fact that in this regime the number of servers is of the same order as the typical queue‐length.