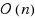Golumbic et al. (2006) defined the readability of a monotone Boolean function f to be the minimum integer k such that there exists an ∧-∨‐formula equivalent to f in which each variable appears at most k times. They asked whether there exists a polynomial‐time algorithm, which given a monotone Boolean function f, in CNF or DNF form, checks whether f is a read‐k function, for a fixed k. In this paper, we partially answer this question already for k=2 by showing that it is NP‐hard to decide if a given monotone formula represents a read‐twice function. It follows also from our reduction that it is NP‐hard to approximate the readability of a given monotone Boolean function f:{0,1}
n
→{0,1} within a factor of
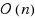. We also give tight sublinear upper bounds on the readability of a monotone Boolean function given in CNF (or DNF) form, parameterized by the number of terms in the CNF and the maximum size in each term, or more generally the maximum number of variables in the intersection of any constant number of terms. When the variables of the DNF can be ordered so that each term consists of a set of consecutive variables, we give much tighter logarithmic bounds on the readability.
