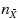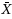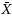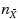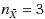The
 and CUSUM control charts are used most widely for monitoring the mean of a quality characteristic x. This article studies the sample sizes
and CUSUM control charts are used most widely for monitoring the mean of a quality characteristic x. This article studies the sample sizes
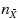 and n
CUSUM
of these two charts in the domain of statistical design. However, the study takes the important sampling inspection cost (including the variable and fixed cost components) into consideration. The chart performance will be measured by a weighted average ATS (Average Time to Signal). There are two interesting findings based on the results of this study: (1) The
and n
CUSUM
of these two charts in the domain of statistical design. However, the study takes the important sampling inspection cost (including the variable and fixed cost components) into consideration. The chart performance will be measured by a weighted average ATS (Average Time to Signal). There are two interesting findings based on the results of this study: (1) The
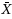 chart becomes more statistically effective for detecting mean shifts when the fixed sampling cost cannot be neglected and/or when the mean shift range is small. If
chart becomes more statistically effective for detecting mean shifts when the fixed sampling cost cannot be neglected and/or when the mean shift range is small. If
 and n
CUSUM
are set as 4 and 1, respectively, based on some conventional wisdom, the simple
and n
CUSUM
are set as 4 and 1, respectively, based on some conventional wisdom, the simple
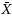 chart often outperforms the more complicated CUSUM chart from an overall viewpoint. (2) Under all circumstances, the overall statistical performance of both charts can be improved, or significantly improved, by the optimization design. The optimal values of
chart often outperforms the more complicated CUSUM chart from an overall viewpoint. (2) Under all circumstances, the overall statistical performance of both charts can be improved, or significantly improved, by the optimization design. The optimal values of
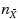 and n
CUSUM
depend on the ratio between the fixed and variable sampling costs, the range of the mean shift, and the in‐control Average Time to Signal. For the general cases, the best sample sizes are
and n
CUSUM
depend on the ratio between the fixed and variable sampling costs, the range of the mean shift, and the in‐control Average Time to Signal. For the general cases, the best sample sizes are
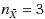 or 4, and n
CUSUM
=2 or 3.
or 4, and n
CUSUM
=2 or 3.