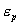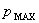Exact and heuristic algorithms of dynamic programming for combinatorial optimization problem

The main difficulty arising in using dynamic programming to solve combinatorial optimization comes from the enormous number of vertices of the state space graph corresponding to the recursion defined. The size of this graph affects both the memory amount and computational time required by any algorithm, making it useless to solve real problems. In this paper an iterative dynamic programming procedure is proposed that, at each iteration p, extracts from the state space graph a partial subgraph having limited dimensions where it looks for the optimal solution. At each iteration the procedure computes the value which estimates the maximum distance from optimality of the produced solution; the succession of values is non increasing. The procedure can be used either to determine the optimal problem solution or a heuristic one in case a maximum number of iterations is given. In this last case represents the maximum distance from optimality of the solution obtained. The procedure is first illustrated for a general combinatorial optimization problem, then it is applied to the Traveling Salesman Problem with time constraints. For this problem, the computational results obtained for some test cases are presented to show the efficiency of the proposed algorithm.