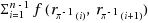On VLSI interconnect optimization and linear ordering problem

Some well‐known VLSI interconnect optimizations problems for timing, power and cross‐coupling noise immunity share a property that enables mapping them into a specialized Linear Ordering Problem (LOP). Unlike the general LOP problem which is NP‐complete, this paper proves that the specialized one has a closed‐form solution. Let f(x,y):ℝ²→ℝ be symmetric, non‐negative, defined for x≥0 and y≥0, and let f(x,y) be twice differentiable, satisfying ∂ ² f(x,y)/∂x∂y<0. Let π be a permutation of {1,…,n}. The specialized LOP comprises n objects, each associated with a real value parameter r i , 1≤i≤n, and a cost f(r i ,r j ) associated to any two objects if |π(i)−π(j)|=1,1≤i,j≤n, and f(r i ,r j )=0 otherwise. We show that the permutation π which minimizes ${\Sigma }_{i=1}^{n‐1}f(r_{{\pi }^{‐1}(i)},r_{{\pi }^{‐1}(i+1)})$ , called ‘symmetric hill’, is determined upfront by the relations between the parameter values r i .