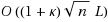Corrector‐predictor methods for sufficient linear complementarity problems

We present a new corrector‐predictor method for solving sufficient linear complementarity problems for which a sufficiently centered feasible starting point is available. In contrast with its predictor‐corrector counterpart proposed by Miao, the method does not depend on the handicap κ of the problem. The method has $O((1+\kappa )\sqrt{n}L)$ ‐iteration complexity, the same as Miao’s method, but our error estimates are sightly better. The algorithm is quadratically convergent for problems having a strictly complementary solution. We also present a family of infeasible higher order corrector‐predictor methods that are superlinearly convergent even in the absence of strict complementarity. The algorithms of this class are globally convergent for general positive starting points. They have $O((1+\kappa )\sqrt{n}L)$ ‐iteration complexity for feasible, or ‘almost feasible’, starting points and O((1+κ)² nL)‐iteration complexity for ‘sufficiently large’ infeasible starting points.