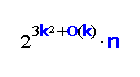Fast Evaluation of Interlace Polynomials on Graphs of Bounded Treewidth

We consider the multivariate interlace polynomial introduced by Courcelle ( 2008), which generalizes several interlace polynomials defined by Arratia, Bollobás, and Sorkin (2004) and by Aigner and van der Holst (2004). We present an algorithm to evaluate the multivariate interlace polynomial of a graph with n vertices given a tree decomposition of the graph of width k. The best previously known result (Courcelle, 2008) employs a general logical framework and leads to an algorithm with running time f(k)·n, where f(k) is doubly exponential in k. Analyzing the GF(2)‐rank of adjacency matrices in the context of tree decompositions, we give a faster and more direct algorithm. Our algorithm uses $2^{3k^2+O(k)}\cdot n$ arithmetic operations and can be efficiently implemented in parallel.