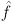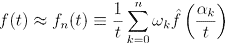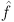A unified framework for numerically inverting Laplace transforms

We introduce and investigate a framework for constructing algorithms to invert Laplace transforms numerically. Given a Laplace transform 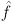$$\widehat{f}$$ of a complex-valued function of a nonnegative real-variable, f, the function f is approximated by a finite linear combination of the transform values; i.e., we use the inversion formula 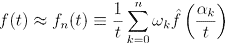$f\left(t\right)\approx f_n\left(t\right)\equiv \frac{1}{t}\underset{k=0}{\overset{n}{\Sigma }}{\omega }_k\widehat{f}\left(\frac{{\alpha }_k}{t}\right)$ , 0 <t<∞, where the weights ωk and nodes αk are complex numbers, which depend on n, but do not depend on the transform $$\widehat{f}$$ 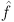or the time argument t. Many different algorithms can be put into this framework, because it remains to specify the weights and nodes. We examine three one-dimensional inversion routines in this framework: the Gaver-Stehfest algorithm, a version of the Fourier-series method with Euler summation, and a version of the Talbot algorithm, which is based on deforming the contour in the Bromwich inversion integral. We show that these three building blocks can be combined to produce different algorithms for numerically inverting two-dimensional Laplace transforms, again all depending on the single parameter n. We show that it can be advantageous to use different one-dimensional algorithms in the inner and outer loops.