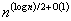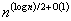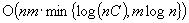| Article ID: | iaor19912119 |
| Country: | United States |
| Volume: | 16 |
| Start Page Number: | 272 |
| End Page Number: | 291 |
| Publication Date: | Mar 1991 |
| Journal: | Mathematics of Operations Research |
| Authors: | Tarjan Robert E. |
| Keywords: | computational analysis |
The paper studies the number of pivots required by the primal network simplex algorithm to solve the minimum-cost circulation problem. A pivot selection rule, with a bound of