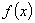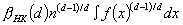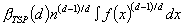| Article ID: | iaor19911711 |
| Country: | United States |
| Volume: | 16 |
| Issue: | 1 |
| Start Page Number: | 72 |
| End Page Number: | 89 |
| Publication Date: | Feb 1991 |
| Journal: | Mathematics of Operations Research |
| Authors: | Bertsimas Dimitris J., Goemans Michel X. |
| Keywords: | computational analysis, programming: travelling salesman |
The authors analyze probabilistically the classical Held-Karp lower bound derived from the 1-tree relaxation for the Euclidean traveling salesman problem (ETSP). They prove that, if