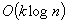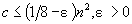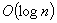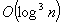| Article ID: | iaor1997989 |
| Country: | Netherlands |
| Volume: | 57 |
| Issue: | 2/3 |
| Start Page Number: | 193 |
| End Page Number: | 212 |
| Publication Date: | Feb 1995 |
| Journal: | Discrete Applied Mathematics |
| Authors: | Kuera Ludk |
| Keywords: | computational analysis |
The paper studies the expected time complexity of two graph partitioning problems: the graph coloring and the cut into equal parts. If