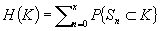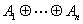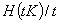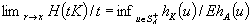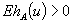| Article ID: | iaor1997317 |
| Country: | United Kingdom |
| Volume: | 27 |
| Issue: | 4 |
| Start Page Number: | 931 |
| End Page Number: | 942 |
| Publication Date: | Dec 1995 |
| Journal: | Advances in Applied Probability |
| Authors: | Molchanov Ilya S., Omey Edward, Kozarovitzky Eugene |
| Keywords: | stochastic processes |
A set-valued analog of the elementary renewal theorem for Minkowski sums of random closed sets is considered. The corresponding renewal function is defined as