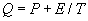Potentially unlimited variance reduction in importance sampling of Markov chains

The authors consider the application of importance sampling in steady-state simulations of finite Markov chains. They show that, for a large class of performance measures, there is a choice of the alternative transition matrix for which the ratio of the variance of the importance sampling estimator to the variance of the naive simulation estimator converges to zero as the sample path length goes to infinity. Obtaining this ‘optimal’ transition matrix involves computing the performance measure of interest, so the optimal matrix cannot be computed in precisely those situations where simulation is required to estimate steady-state performance. However, our results show that alternative transition matrices of the form , where P is the original transition matrix and T is the sample path length, can be expected to provide good results. Moreover, the authorsj provide an iterative algorithm for obtaining alternative transition matrices of this form that converge to the optimal matrix as the number of iterations increases, and present an example that shows that spending some computer time iterating this algorithm and then conducting the simulation with the resulting alternative transition matrix may provide considerable variance reduction when compared to naive simulation.