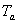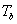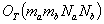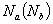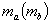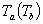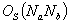A tree embedded in a plane can be characterized as an unrooted and cyclically ordered tree (CO-tree). This paper describes new definitions of three distances between CO-trees and their computing methods. The proposed distances are based on the Tai mapping, the structure preserving mapping and the strongly structure preserving mapping, respectively, and are called the Tai distance (TD), the structure preserving distance (SPD) and the strongly structure preserving distance (SSPD), respectively. The definitions of distances and their computing methods are simpler than those of the old definitions and computing methods, respectively. TD and SPD by the new definitions are more sensitive than those by the old ones, and SSPDs by both definitions are equivalent. The time complexities of computing TD, SPD and SSPD between CO-trees 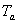 and
and 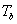 are
are  ,
,  and
and 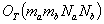 , respectively, where
, respectively, where 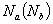 and
and 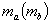 are the number of vertices in tree
are the number of vertices in tree  and the maximum degree of a vertex in
and the maximum degree of a vertex in 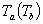 , respectively. The space complexities of these methods are
, respectively. The space complexities of these methods are 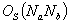 .
.