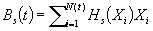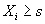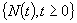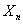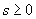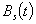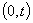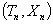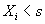In this paper a class of correlated cumulative processes,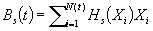 
, is studied with excess level increments 
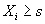, where 
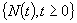, is the counting process generated by the renewal sequence 
and 
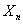are correlated for given n, 
is the Heaviside function and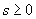 
is a given constant. Several useful results, for the distributions of 
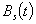, and that of the number of excess (non-excess) increments on 
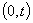and the corresponding means, are derived. First passage time problems are also discussed and various asymptotic properties of the processes are obtained. Transform results, by applying a flexible form for the joint distribution of correlated pairs 
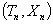are derived and inverted. The case of non-excess level increments, 
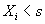, is also considered. Finally, applications to known stochastic shock and pro-rata warranty models are given.
