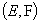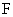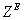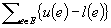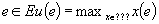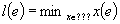| Article ID: | iaor19961811 |
| Country: | Japan |
| Volume: | 38 |
| Issue: | 3 |
| Start Page Number: | 362 |
| End Page Number: | 375 |
| Publication Date: | Sep 1995 |
| Journal: | Journal of the Operations Research Society of Japan |
| Authors: | Fujishige Satoru, Naitoh Takeshi, Ando Kazutoshi |
| Keywords: | optimization, programming: integer |
The authors present a greedy algorithm for minimizing a separable convex function over a finite jump system