
| Article ID: | iaor19961696 |
| Country: | Japan |
| Volume: | 38 |
| Issue: | 3 |
| Start Page Number: | 289 |
| End Page Number: | 300 |
| Publication Date: | Sep 1995 |
| Journal: | Journal of the Operations Research Society of Japan |
| Authors: | Yoshimoto Kazuho, Yagi Eiichiro |
| Keywords: | decision, systems |
In the field of system engineering, numerous proposals have been made for structural modeling. In the many structural modeling methods, the first process is to make a binary relation matrix. This process is difficult because the number of questions to extract binary relation is 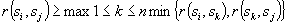
.gif)
.gif)
.gif)
.gif)
.gif)
.gif)
.gif)
.gif)