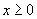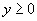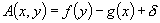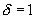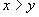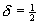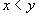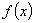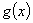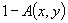This paper considers a two-person constant sum game in which a prize with value 1 goes to the player who bids the most for it, the cost of each player's bid being a known, increasing function of its magnitude. Specifically, if player 1 bids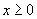 
and player 2 bids 
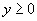, the payoff is 
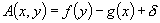where 
if 
, 
if 
and 
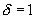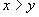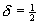if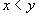 
. The bids might be direct [in which case f( y)=y and g(x)=x], but applications also include situations where x and y represent some physical quantity, with 
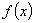and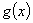 
being the costs of achievement. The payoff to player 2 is 
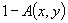. In their most abstract form, competitive design problems can sometimes be expressed as excess games. The essential feature must be a contest involving some scalar measure of ‘strength’ with the stronger system being the winner in any individual combat. For example, y might be a thickness of armor, and x the thickness of armor that can be penetrated by a weapon or tooth. Alternatively x and y might represent any of several electronic quantities that determine whether communication through jamming is possible, or x and y might be top speeds. It is found that excess games generally have mixed strategy solutions, a conclusion consistent with the observed diversity of military hardware and biological species.
