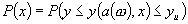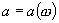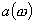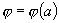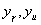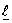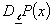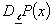| Article ID: | iaor1996612 |
| Country: | United States |
| Volume: | 30 |
| Issue: | 3/6 |
| Start Page Number: | 361 |
| End Page Number: | 382 |
| Publication Date: | Sep 1995 |
| Journal: | Computers & Mathematics with Applications |
| Authors: | Marti K. |
| Keywords: | quality & reliability |
In reliability-oriented design and optimization of engineering systems, one needs various derivatives of the probability of systems survival