
| Article ID: | iaor1996281 |
| Country: | Netherlands |
| Volume: | 56 |
| Issue: | 2/3 |
| Start Page Number: | 137 |
| End Page Number: | 155 |
| Publication Date: | Jan 1995 |
| Journal: | Discrete Applied Mathematics |
| Authors: | Masuyama Shigeru, Cheng Peng |
| Keywords: | probability |
For a probabilistic graph 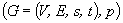
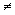
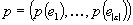
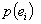
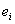

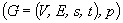
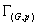
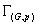
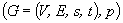
.gif)