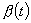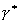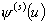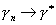| Article ID: | iaor1995793 |
| Country: | United States |
| Volume: | 19 |
| Issue: | 2 |
| Start Page Number: | 410 |
| End Page Number: | 433 |
| Publication Date: | May 1994 |
| Journal: | Mathematics of Operations Research |
| Authors: | Asmussen Soren, Rolski Tomasz |
| Keywords: | finance & banking, risk |
A risk process with the claim arrival intensity