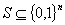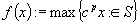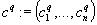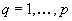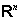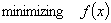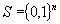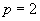| Article ID: | iaor1995308 |
| Country: | Netherlands |
| Volume: | 42 |
| Issue: | 2/3 |
| Start Page Number: | 139 |
| End Page Number: | 145 |
| Publication Date: | Apr 1993 |
| Journal: | Discrete Applied Mathematics |
| Authors: | Hamacher Horst W., Murty Katta G., Chung Sung-Jin, Maffioli Francesco |
| Keywords: | combinatorial analysis |
The authors consider combinatorial optimization problems with a feasible solution set