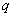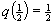| Article ID: | iaor19942321 |
| Country: | United Kingdom |
| Volume: | 3 |
| Issue: | 1 |
| Start Page Number: | 41 |
| End Page Number: | 58 |
| Publication Date: | Apr 1994 |
| Journal: | Journal of Multi-Criteria Decision Analysis |
| Authors: | Dyckerhoff R. |
In expected utility many results have been derived that give necessary and/or sufficient conditions for a multivariate utility function to be decomposable into lower-dimensional functions. In particular, multilinear, multiplicative and additive decompositions have been widely discussed. These utility functions can be more easily assessed in practical situations. This paper presents a theory of decomposition in the context of non-additive expected utility such as anticipated utility or Choquet expected utility. It shows that many of the results used in conventional expected utility carry over to these more general frameworks. If preferences over lotteries depend only on the marginal probability distributions, then in expected utility the utility function is additively decomposable. It is shown that in anticipated utility the marginality condition implies not only that the utility function is additively decomposable but also that the distortion function is the identify function. It is further demonstrated that a decision maker who is bivariate risk neutral has a utility function that is additively decomposable and a distortion function