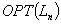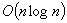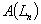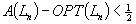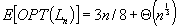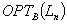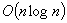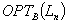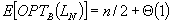| Article ID: | iaor1988921 |
| Country: | United States |
| Volume: | 18 |
| Issue: | 1 |
| Start Page Number: | 166 |
| End Page Number: | 185 |
| Publication Date: | Feb 1989 |
| Journal: | SIAM Journal On Control and Optimization |
| Authors: | Coffman E.G., Lagarias J.C. |
| Keywords: | scheduling |
This paper gives a probabilistic performance analysis of simple algorithms for packing lists