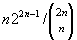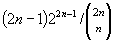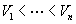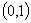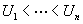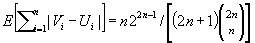| Article ID: | iaor1994711 |
| Country: | United States |
| Volume: | 18 |
| Issue: | 3 |
| Start Page Number: | 566 |
| End Page Number: | 577 |
| Publication Date: | Aug 1993 |
| Journal: | Mathematics of Operations Research |
| Authors: | Harel Arie |
| Keywords: | combinatorial analysis |
A simple random walk with reflected origin is considered. The walk starts at the origin and it must return to the origin at time 2