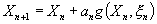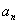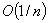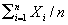| Article ID: | iaor1994391 |
| Country: | United States |
| Volume: | 31 |
| Issue: | 4 |
| Start Page Number: | 1045 |
| End Page Number: | 1062 |
| Publication Date: | Jul 1993 |
| Journal: | SIAM Journal on Control and Optimization |
| Authors: | Kushner Harold J., Yang Jichuan |
| Keywords: | computational analysis |
Consider the stochastic approximation algorithm