A self‐bilinear map is a bilinear map where the domain and target groups are identical. In this paper, we introduce a self‐bilinear map with auxiliary information which is a weaker variant of a self‐bilinear map, construct it based on indistinguishability obfuscation and prove that a useful hardness assumption holds with respect to our construction under the factoring assumption. From our construction, we obtain a multilinear map with interesting properties: the level of multilinearity is not bounded in the setup phase, and representations of group elements are compact, i.e., their size is independent of the level of multilinearity. This is the first construction of a multilinear map with these properties. Note, however, that to evaluate the multilinear map, auxiliary information is required. As applications of our multilinear map, we construct multiparty non‐interactive key‐exchange and distributed broadcast encryption schemes where the maximum number of users is not fixed in the setup phase. Besides direct applications of our self‐bilinear map, we show that our technique can also be used for constructing somewhat homomorphic encryption based on indistinguishability obfuscation and the
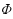‐hiding assumption.
