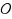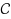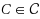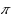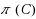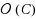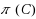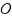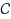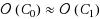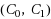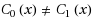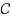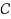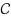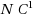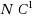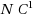On Virtual Grey Box Obfuscation for General Circuits

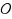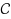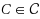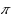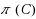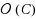An obfuscator $\mathcal{O}$ is Virtual Grey Box (VGB) for a class $\mathcal{C}$ of circuits if, for any $C\in \mathcal{C}$ and any predicate $\mathit{\pi }$ , deducing $\mathit{\pi }(C)$ given $\mathcal{O}(C)$ is tantamount to deducing 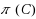$\mathit{\pi }(C)$ given unbounded computational resources and polynomially many oracle queries to C. VGB obfuscation is often significantly more meaningful than indistinguishability obfuscation (IO). In fact, for some circuit families of interest VGB is equivalent to full‐fledged Virtual Black Box obfuscation. We investigate the feasibility of obtaining VGB obfuscation for general circuits. We first formulate a natural strengthening of IO, called strong IO (SIO). 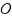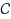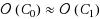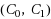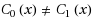Essentially, $\mathcal{O}$ is SIO for class $\mathcal{C}$ if $\mathcal{O}(C_0)\approx \mathcal{O}(C_1)$ whenever the pair $(C_0,C_1)$ is taken from a distribution over $\mathcal{C}$ where, for all x, $C_0(x)\ne C_1(x)$ only with negligible probability. We then show that an obfuscator is VGB for a class 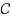$\mathcal{C}$ if and only if it is SIO for 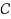$\mathcal{C}$ . This result is unconditional and holds for any 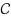$\mathcal{C}$ . We also show that, for some circuit collections, SIO implies virtual black‐box obfuscation. Finally, we formulate a slightly stronger variant of the semantic security property of graded encoding schemes [Pass‐Seth‐Telang Crypto 14], and show that existing obfuscators, such as the obfuscator of Barak et al. [Eurocrypt 14], are SIO for all circuits in 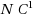$N{C}^1$ , assuming that the underlying graded encoding scheme satisfies our variant of semantic security. Put together, we obtain VGB obfuscation for all 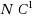$N{C}^1$ circuits under assumptions that are almost the same as those used by Pass et al. to obtain IO for 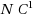$N{C}^1$ circuits. We also observe that VGB obfuscation for all polynomial‐size circuits implies the existence of semantically‐secure graded encoding schemes with limited functionality known as jigsaw puzzles.