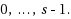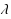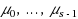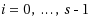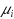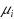We present a tandem network of queues
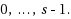 Customers arrive at queue 0 according to a Poisson process with rate
Customers arrive at queue 0 according to a Poisson process with rate
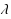 . There are s independent batch service processes at exponential rates
. There are s independent batch service processes at exponential rates
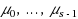 . Service process i,
. Service process i,
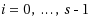 , at rate
, at rate
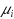 is such that all customers of all queues
is such that all customers of all queues
 simultaneously receive service and move to the next queue. We show that this system has a geometric product‐form steady‐state distribution. Moreover, we determine the service allocation that minimizes the waiting time in the system and state conditions to approximate such optimal allocations. Our model is motivated by applications in wireless sensor networks, where s observations from different sensors are collected for data fusion. We demonstrate that both optimal centralized and decentralized sensor scheduling can be modeled by our queueing model by choosing the values of
simultaneously receive service and move to the next queue. We show that this system has a geometric product‐form steady‐state distribution. Moreover, we determine the service allocation that minimizes the waiting time in the system and state conditions to approximate such optimal allocations. Our model is motivated by applications in wireless sensor networks, where s observations from different sensors are collected for data fusion. We demonstrate that both optimal centralized and decentralized sensor scheduling can be modeled by our queueing model by choosing the values of
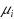 appropriately. We quantify the performance gap between the centralized and decentralized schedules for arbitrarily large sensor networks.
appropriately. We quantify the performance gap between the centralized and decentralized schedules for arbitrarily large sensor networks.