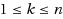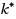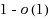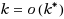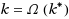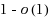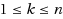Partial Sorting Problem on Evolving Data

In this paper we investigate the top‐k‐selection problem, i.e. to determine and sort the top k elements, in the dynamic data model. Here dynamic means that the underlying total order evolves over time, and that the order can only be probed by pair‐wise comparisons. It is assumed that at each time step, only one pair of elements can be compared. This assumption of restricted access is reasonable in the dynamic model, especially for massive data sets where it is impossible to access all the data before the next change occurs. Previously only two special cases were studied (Anagnostopoulos et al. in 36th international colloquium on automata, languages and programming (ICALP). LNCS, vol 5566, pp 339–350, 2009) in this model: selecting the element of a given rank, and sorting all elements. This paper systematically deals with 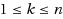$1\le k\le n$ . Specifically, we identify the critical point 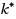$k^{\ast }$ such that the top‐k‐selection problem can be solved error‐free with probability 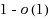$1‐o(1)$ if and only if 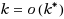$k=o(k^{\ast })$ . A lower bound of the error when 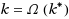$k=\mathit{\Omega }(k^{\ast })$ is also determined, which actually is tight under some conditions. In contrast, we show that the top‐k‐set problem, which means finding the top k elements without sorting them, can be solved error‐free with probability 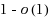$1‐o(1)$ for all 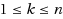$1\le k\le n$ . Additionally, we consider some extensions of the dynamic data model and show that most of these results still hold.