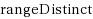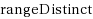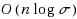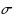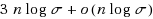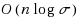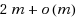A Framework for Space-Efficient String Kernels

String kernels are typically used to compare genome‐scale sequences whose length makes alignment impractical, yet their computation is based on data structures that are either space‐inefficient, or incur large slowdowns. We show that a number of exact kernels on pairs of strings of total length n, like the k‐mer kernel, the substrings kernels, a number of length‐weighted kernels, the minimal absent words kernel, and kernels with Markovian corrections, can all be computed in O(nd) time and in o(n) bits of space in addition to the input, using just a $\mathtt{rangeDistinct}$ data structure on the Burrows–Wheeler transform of the input strings that takes O(d) time per element in its output. The same bounds hold for a number of measures of compositional complexity based on multiple values of k, like the k‐mer profile and the k‐th order empirical entropy, and for calibrating the value of k using the data. 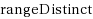All such algorithms become O(n) using a suitable implementation of the $\mathtt{rangeDistinct}$ data structure, and by concatenating them to a suitable BWT construction algorithm, we can compute all the mentioned kernels and complexity measures, directly from the input strings, in O(n) time and in 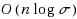$O(nlog\mathit{\sigma })$ bits of space in addition to the input, where 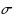$\mathit{\sigma }$ is the size of the alphabet. Using similar data structures, we also show how to build a compact representation of the variable‐length Markov chain of a string T of length n, that takes just 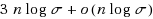$3nlog\mathit{\sigma }+o(nlog\mathit{\sigma })$ bits of space, and that can be learnt in randomized O(n) time using 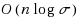$O(nlog\mathit{\sigma })$ bits of space in addition to the input. Such model can then be used to assign a probability to a query string S of length m in O(m) time and in 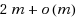$2m+o(m)$ bits of additional space, thus providing an alternative, compositional measure of the similarity between S and T that does not require alignment.