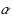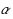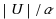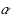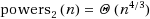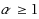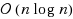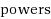In this paper we consider substrings of an unrooted edge‐labeled tree, which are defined as the composite labels of simple paths. We study how the number of distinct repetitive substrings depends on their exponent
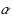 . An
. An
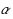 ‐power is defined as a string U with an (integral, not necessarily shortest) period
‐power is defined as a string U with an (integral, not necessarily shortest) period
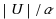 . For example, squares are 2‐powers and cubes are 3‐powers. We investigate the asymptotic growth of the maximal number
. For example, squares are 2‐powers and cubes are 3‐powers. We investigate the asymptotic growth of the maximal number
 of distinct
of distinct
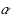 ‐powers occurring as substrings of a tree with n nodes. The maximum number of such powers behaves much unlike in strings. In a previous work (CPM 2012. LNCS, vol 7354. Springer, Berlin, pp 27–40, 2012. It was proved that the number of different squares in a tree is
‐powers occurring as substrings of a tree with n nodes. The maximum number of such powers behaves much unlike in strings. In a previous work (CPM 2012. LNCS, vol 7354. Springer, Berlin, pp 27–40, 2012. It was proved that the number of different squares in a tree is
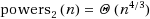 . We extend this result and analyze powers of arbitrary rational exponent
. We extend this result and analyze powers of arbitrary rational exponent
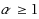 . We identify two phase‐transition thresholds:
for
;
for
;
for
.
This is a full version of a paper presented at CPM 2015. LNCS, vol 9133. Springer, Berlin, pp 284–294, 2015. Compared to the earlier version, we improve our main technical contribution, i.e., the upper bound on the number of cubes in a tree, from
. We identify two phase‐transition thresholds:
for
;
for
;
for
.
This is a full version of a paper presented at CPM 2015. LNCS, vol 9133. Springer, Berlin, pp 284–294, 2015. Compared to the earlier version, we improve our main technical contribution, i.e., the upper bound on the number of cubes in a tree, from
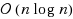 to
to
 . This lets us obtain a tight asymptotic characterization of the
. This lets us obtain a tight asymptotic characterization of the
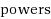 function.
function.