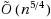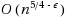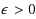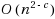Quantum Algorithm for Triangle Finding in Sparse Graphs

This paper presents a quantum algorithm for triangle finding over sparse graphs that improves over the previous best quantum algorithm for this task by Buhrman et al. (SIAM J Comput 34(6):1324–1330, 2005). Our algorithm is based on the recent $\tilde{O}(n^{5/4})$ ‐query algorithm given by Le Gall (Proceedings of the 55th IEEE annual symposium on foundations of computer science, pp 216–225, 2014) for triangle finding over dense graphs (here n denotes the number of vertices in the graph). We show in particular that triangle finding can be solved with $O(n^{5/4‐\mathit{ϵ}})$ queries for some constant $\mathit{ϵ}>0$ whenever the graph has at most $O(n^{2‐c})$ edges for some constant $c>0$ .