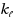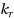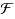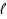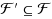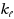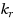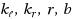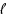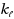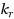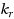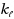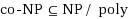Multivariate Complexity Analysis of Geometric RED BLUE SET COVER

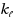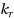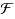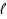We investigate the parameterized complexity of Generalized Red Blue Set Cover (Gen‐RBSC), a generalization of the classic Set Cover problem and the more recently studied Red Blue Set Cover problem. Given a universe U containing b blue elements and r red elements, positive integers $k_{𝓁}$ and $k_r$ , and a family $\mathcal{F}$ of $𝓁$ sets over U, the Gen‐RBSC problem is to decide whether there is a subfamily 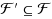${\mathcal{F}}^{\prime }\subseteq \mathcal{F}$ of size at most 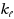$k_{𝓁}$ that covers all blue elements, but at most 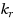$k_r$ of the red elements. This generalizes Set Cover and thus in full generality it is intractable in the parameterized setting. In this paper, we study a geometric version of this problem, called Gen‐RBSC‐lines, where the elements are points in the plane and sets are defined by lines. 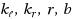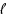We study this problem for an array of parameters, namely, $k_{𝓁},k_r,r,b$ , and $𝓁$ , and all possible combinations of them. For all these cases, we either prove that the problem is W‐hard or show that the problem is fixed parameter tractable (FPT). 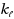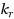In particular, on the algorithmic side, our study shows that a combination of $k_{𝓁}$ and $k_r$ gives rise to a nontrivial algorithm for Gen‐RBSC‐lines. On the hardness side, we show that the problem is para‐NP‐hard when parameterized by 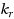$k_r$ , and W[1]‐hard when parameterized by 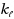$k_{𝓁}$ . Finally, for the combination of parameters for which Gen‐RBSC‐lines admits FPT algorithms, we ask for the existence of polynomial kernels. 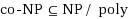We are able to provide a complete kernelization dichotomy by either showing that the problem admits a polynomial kernel or that it does not contain a polynomial kernel unless $\text{co‐NP}\subseteq \text{NP}/\text{poly}$ .