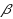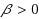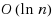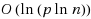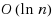Metric Decompositions of Path-Separable Graphs

A prominent tool in many problems involving metric spaces is a notion of randomized low‐diameter decomposition. Loosely speaking, 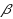$\mathit{\beta }$ ‐decomposition refers to a probability distribution over partitions of the metric into sets of low diameter, such that nearby points (parameterized by 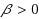$\mathit{\beta }>0$ ) are likely to be ‘clustered’ together. Applying this notion to the shortest‐path metric in edge‐weighted graphs, it is known that n‐vertex graphs admit an 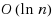$O(lnn)$ ‐padded decomposition (Bartal, 37th annual symposium on foundations of computer science. IEEE, pp 184–193, 1996), and that excluded‐minor graphs admit O(1)‐padded decomposition (Klein et al., 25th annual ACM symposium on theory of computing, pp 682–690, 1993; Fakcharoenphol and Talwar, J Comput Syst Sci 69(3), 485–497, 2004; Abraham et al., Proceedings of the 46th annual ACM symposium on theory of computing. STOC ‘14, pp 79–88. ACM, New York, NY, USA, 2014). We design decompositions to the family of p‐path‐separable graphs, which was defined by Abraham and Gavoille (Proceedings of the twenty‐fifth annual acm symposium on principles of distributed computing, PODC ‘06, pp 188–197, 2006) and refers to graphs that admit vertex‐separators consisting of at most p shortest paths in the graph. Our main result is that every p‐path‐separable n‐vertex graph admits an 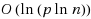$O(ln(plnn))$ ‐decomposition, which refines the 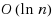$O(lnn)$ bound for general graphs, and provides new bounds for families like bounded‐treewidth graphs. Technically, our clustering process differs from previous ones by working in (the shortest‐path metric of) carefully chosen subgraphs.