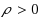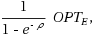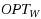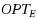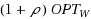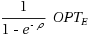Trading Off Worst and Expected Cost in Decision Tree Problems

We characterize the best possible trade‐off achievable when optimizing the construction of a decision tree with respect to both the worst and the expected cost. It is known that a decision tree achieving the minimum possible worst case cost can behave very poorly in expectation (even exponentially worse than the optimal), and the vice versa is also true. Led by applications where deciding which optimization criterion might not be easy, several authors recently have focussed on the bicriteria optimization of decision trees. Here we sharply define the limits of the best possible trade‐offs between expected and worst case cost. More precisely, we show that for every $\mathit{\rho }>0$ there is a decision tree D with worst testing cost at most $(1+\mathit{\rho }){\mathit{OPT}}_W$ and expected testing cost at most $\frac{1}{1‐e^{‐\mathit{\rho }}}{\mathit{OPT}}_E,$ where ${\mathit{OPT}}_W$ and ${\mathit{OPT}}_E$ denote the minimum worst testing cost and the minimum expected testing cost of a decision tree for the given instance. We also show that this is the best possible trade‐off in the sense that there are infinitely many instances for which we cannot obtain a decision tree with both worst testing cost smaller than $(1+\mathit{\rho }){\mathit{OPT}}_W$ and expected testing cost smaller than $\frac{1}{1‐e^{‐\mathit{\rho }}}{\mathit{OPT}}_E$ .