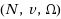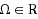| Article ID: | iaor20173389 |
| Volume: | 86 |
| Issue: | 1 |
| Start Page Number: | 149 |
| End Page Number: | 170 |
| Publication Date: | Aug 2017 |
| Journal: | Mathematical Methods of Operations Research |
| Authors: | Radzik Tadeusz |
| Keywords: | simulation |
We propose a new more general approach to TU‐games and their efficient values, significantly different from the classical one. It leads to extended TU‐games described by a triplet