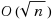The Book Thickness of 1-Planar Graphs is Constant

In a book embedding, the vertices of a graph are placed on the ‘spine’ of a book and the edges are assigned to ‘pages’, so that edges on the same page do not cross. In this paper, we prove that every 1‐planar graph (that is, a graph that can be drawn on the plane such that no edge is crossed more than once) admits an embedding in a book with constant number of pages. To the best of our knowledge, the best non‐trivial previous upper‐bound is $O(\sqrt{n})$ , where n is the number of vertices of the graph.