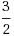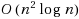Set It and Forget It: Approximating the Set Once Strip Cover Problem

We consider the Set Once Strip Cover problem, in which n wireless sensors are deployed over a one‐dimensional region. Each sensor has a fixed battery that drains in inverse proportion to a radius that can be set just once, but activated at any time. The problem is to find an assignment of radii and activation times that maximizes the length of time during which the entire region is covered. We show that this problem is NP‐hard. In addition, we show that RoundRobin, the algorithm in which the sensors take turns covering the entire region, has a tight approximation guarantee of 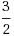$\frac{3}{2}$ . This result also applies to the more general Strip Cover problem, in which each radius may be set finitely‐many times. Moreover, we show that the more general class of duty cycle algorithms, in which groups of sensors take turns covering the entire region, can do no better. Finally, we give an 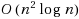$O(n^{2}logn)$ ‐time optimization algorithm for the related Set Radius Strip Cover problem, in which sensors must be activated immediately.