Caching (also known as paging) is a classical problem concerning page replacement policies in two‐level memory systems. General caching is the variant with pages of different sizes and fault costs. The strong NP‐hardness of its two important cases, the fault model (each page has unit fault cost) and the bit model (each page has the same fault cost as size) has been established, but under the assumption that there are pages as large as half of the cache size. We prove that this already holds when page sizes are bounded by a small constant: The bit and fault models are strongly NP‐complete even when page sizes are limited to
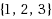. Considering only the decision versions of the problems, general caching is equivalent to the unsplittable flow on a path problem and therefore our results also improve the hardness results about this problem.
