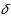We study a
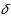shock and wear model in which the system can fail due to the frequency of the shocks caused by external conditions, or aging and accumulated wear caused by intrinsic factors. The external shocks occur according to a Bernoulli process, i.e., the inter‐arrival times between two consecutive shocks follow a geometric distribution. Once the system fails, it can be repaired immediately. If the system is not repairable in a pre‐specific time D, it can be replaced by a new one to avoid the unnecessary expanses on repair. On the other hand, the system can also be replaced whenever its number of repairs exceeds N. Given that infinite operating and repair times are not commonly encountered in practical situations, both of these two random variables are supposed to obey general discrete distribution with finite support. Replacing the finite support renewal distributions with appropriate phase‐type (PH) distributions and using the closure property associated with PH distribution, we formulate the maximum repair time replacement policy and obtain analytically the long‐run average cost rate. Meanwhile, the optimal replacement policy is also numerically determined by implementing a two‐dimensional‐search process.
