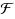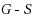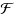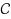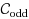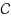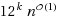Let
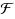 be a family of graphs. Given an n‐vertex input graph G and a positive integer k, testing whether G has a vertex subset S of size at most k, such that
be a family of graphs. Given an n‐vertex input graph G and a positive integer k, testing whether G has a vertex subset S of size at most k, such that
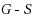 belongs to
belongs to
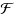 , is a prototype vertex deletion problem. These type of problems have attracted a lot of attention in recent times in the domain of parameterized complexity. In this paper, we study two such problems; when
, is a prototype vertex deletion problem. These type of problems have attracted a lot of attention in recent times in the domain of parameterized complexity. In this paper, we study two such problems; when
 is either the family of forests of cacti or the family of forests of odd‐cacti. A graph H is called a forest of cacti if every pair of cycles in H intersect on at most one vertex. Furthermore, a forest of cacti H is called a forest of odd cacti, if every cycle of H is of odd length. Let us denote by
is either the family of forests of cacti or the family of forests of odd‐cacti. A graph H is called a forest of cacti if every pair of cycles in H intersect on at most one vertex. Furthermore, a forest of cacti H is called a forest of odd cacti, if every cycle of H is of odd length. Let us denote by
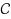 and
and
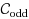 , the families of forests of cacti and forests of odd cacti, respectively. The vertex deletion problems corresponding to
, the families of forests of cacti and forests of odd cacti, respectively. The vertex deletion problems corresponding to
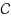 and
and
 are called Diamond Hitting Set and Even Cycle Transversal, respectively. In this paper we design randomized algorithms with worst case run time
are called Diamond Hitting Set and Even Cycle Transversal, respectively. In this paper we design randomized algorithms with worst case run time
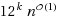 for both these problems. Our algorithms considerably improve the running time for Diamond Hitting Set and Even Cycle Transversal, compared to what is known about them.
for both these problems. Our algorithms considerably improve the running time for Diamond Hitting Set and Even Cycle Transversal, compared to what is known about them.