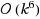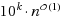A Polynomial Kernel for Block Graph Deletion

In the Block Graph Deletion problem, we are given a graph G on n vertices and a positive integer k, and the objective is to check whether it is possible to delete at most k vertices from G to make it a block graph, i.e., a graph in which each block is a clique. In this paper, we obtain a kernel with 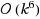$\mathcal{O}(k^6)$ vertices for the Block Graph Deletion problem. This is a first step to investigate polynomial kernels for deletion problems into non‐trivial classes of graphs of bounded rank‐width, but unbounded tree‐width. Our result also implies that Chordal Vertex Deletion admits a polynomial‐size kernel on diamond‐free graphs. For the kernelization and its analysis, we introduce the notion of ‘complete degree’ of a vertex. We believe that the underlying idea can be potentially applied to other problems. 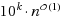We also prove that the Block Graph Deletion problem can be solved in time ${10}^k·n^{\mathcal{O}(1)}$ .