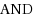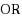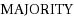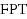Complexity and Approximability of Parameterized MAX-CSPs

We study the optimization version of constraint satisfaction problems (Max‐CSPs) in the framework of parameterized complexity; the goal is to compute the maximum fraction of constraints that can be satisfied simultaneously. In standard CSPs, we want to decide whether this fraction equals one. The parameters we investigate are structural measures, such as the treewidth or the clique‐width of the variable–constraint incidence graph of the CSP instance. We consider Max‐CSPs with the constraint types $\text{AND}$ , $\text{OR}$ , $\text{PARITY}$ , and $\text{MAJORITY}$ , and with various parameters k, and we attempt to fully classify them into the following three cases:

The exact optimum can be computed in $‐{FPT}$ time.

It is W[I] ‐hard to compute the exact optimum, but there is a randomized $‐{FPT}$ approximation scheme ( $‐{FPT}‐{\text{‐}}‐{AS}$ ), which computes a $(1‐\mathit{ϵ})$ ‐approximation in time $f(k,\mathit{ϵ})·\text{poly}(n)$ .

There is no $‐{FPT}‐{\text{‐}}‐{AS}$ unless FPT=W[I].

For the corresponding standard CSPs, we establish $‐{FPT}$ versus ‐hardness results.