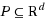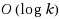Complete‐linkage clustering is a very popular method for computing hierarchical clusterings in practice, which is not fully understood theoretically. Given a finite set
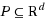of points, the complete‐linkage method starts with each point from P in a cluster of its own and then iteratively merges two clusters from the current clustering that have the smallest diameter when merged into a single cluster. We study the problem of partitioning P into k clusters such that the largest diameter of the clusters is minimized and we prove that the complete‐linkage method computes an O(1)‐approximation for this problem for any metric that is induced by a norm, assuming that the dimension d is a constant. This improves the best previously known bound of
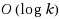due to Ackermann et al. (Algorithmica 69(1):184–215, 2014). Our improved bound also carries over to the k‐center and the discrete k‐center problem.
