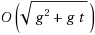Given an undirected, edge‐weighted graph G together with pairs of vertices, called pairs of terminals, the minimum multicut problem asks for a minimum‐weight set of edges such that, after deleting these edges, the two terminals of each pair belong to different connected components of the graph. Relying on topological techniques, we provide a polynomial‐time algorithm for this problem in the case where G is embedded on a fixed surface of genus g (e.g., when G is planar) and has a fixed number t of terminals. The running time is a polynomial of degree
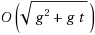in the input size. In the planar case, our result corrects an error in an extended abstract by Bentz (Int. Workshop on Parameterized and Exact Computation, 109–119, 2012). The minimum multicut problem is also a generalization of the multiway cut problem, a.k.a. multiterminal cut problem; even for this special case, no dedicated algorithm was known for graphs embedded on surfaces.
