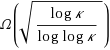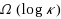| Article ID: | iaor20173033 |
| Volume: | 78 |
| Issue: | 4 |
| Start Page Number: | 1246 |
| End Page Number: | 1262 |
| Publication Date: | Aug 2017 |
| Journal: | Algorithmica |
| Authors: | Azar Yossi, Gilon Oren |
| Keywords: | combinatorial optimization, scheduling, production, queues: applications |
We discuss the well known online job scheduling problem with release times and deadlines, alongside an extended model–buffer management for packets with processing requirements. For job scheduling, an