Extending the Kernel for Planar Steiner Tree to the Number of Steiner Vertices

In the Steiner Tree problem one is given an undirected graph, a subset T of its vertices, and an integer k and the question is whether there is a connected subgraph of the given graph containing all the vertices of T and at most k other vertices. The vertices in the subset T are called terminals and the other vertices are called Steiner vertices. Recently, Pilipczuk et al. (55th IEEE Annual Symposium on Foundations of Computer Science, FOCS, 2014) gave a polynomial kernel for Steiner Tree in planar graphs and graphs of bounded genus, when parameterized by 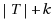$|T|+k$ , the total number of vertices in the constructed subgraph. In this paper we present several polynomial time applicable reduction rules for Steiner Tree in graphs of bounded genus. In an instance reduced with respect to the presented reduction rules, the number of terminals |T| is at most cubic in the number of other vertices k in the subgraph. Hence, using and improving the result of Pilipczuk et al., we give a polynomial kernel for Steiner Tree in graphs of bounded genus for the parameterization by the number k of Steiner vertices in the solution. We give better bounds for Steiner Tree in planar graphs.