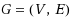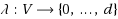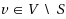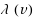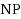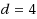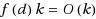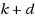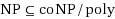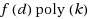In the Vector Connectivity problem we are given an undirected graph
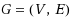 , a demand function
, a demand function
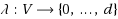 , and an integer k. The question is whether there exists a set S of at most k vertices such that every vertex
, and an integer k. The question is whether there exists a set S of at most k vertices such that every vertex
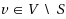 has at least
has at least
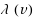 vertex‐disjoint paths to S; this abstractly captures questions about placing servers or warehouses relative to demands. The problem is
vertex‐disjoint paths to S; this abstractly captures questions about placing servers or warehouses relative to demands. The problem is
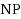 ‐hard already for instances with
‐hard already for instances with
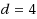 (Cicalese et al., Theoretical Computer Science ‘15), admits a log‐factor approximation (Boros et al., Networks ‘14), and is fixed‐parameter tractable in terms of k (Lokshtanov, unpublished ‘14). We prove several results regarding kernelization and approximation for Vector Connectivity and the variant Vector
d‐Connectivity where the upper bound d on demands is a fixed constant. For Vector
d‐Connectivity we give a factor d‐approximation algorithm and construct a vertex‐linear kernelization, that is, an efficient reduction to an equivalent instance with
(Cicalese et al., Theoretical Computer Science ‘15), admits a log‐factor approximation (Boros et al., Networks ‘14), and is fixed‐parameter tractable in terms of k (Lokshtanov, unpublished ‘14). We prove several results regarding kernelization and approximation for Vector Connectivity and the variant Vector
d‐Connectivity where the upper bound d on demands is a fixed constant. For Vector
d‐Connectivity we give a factor d‐approximation algorithm and construct a vertex‐linear kernelization, that is, an efficient reduction to an equivalent instance with
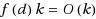 vertices. For Vector Connectivity we have a factor
vertices. For Vector Connectivity we have a factor
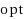 ‐approximation and we can show that it has no kernelization to size polynomial in k or even
‐approximation and we can show that it has no kernelization to size polynomial in k or even
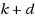 unless
unless
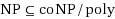 , which shows that
, which shows that
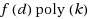 is optimal for Vector
d‐Connectivity. Finally, we give a simple randomized fixed‐parameter algorithm for Vector Connectivity with respect to k based on matroid intersection.
is optimal for Vector
d‐Connectivity. Finally, we give a simple randomized fixed‐parameter algorithm for Vector Connectivity with respect to k based on matroid intersection.