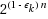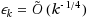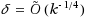| Article ID: | iaor20173026 |
| Volume: | 79 |
| Issue: | 1 |
| Start Page Number: | 29 |
| End Page Number: | 41 |
| Publication Date: | Sep 2017 |
| Journal: | Algorithmica |
| Authors: | Bonacina Ilario, Talebanfard Navid |
| Keywords: | game theory, heuristics |
We consider a proof system intermediate between